Based of COMS 6998-006: Foundations of Blockchains by Tim Roughgarden.

Overview

These notes explain how blockchains work, focusing on consensus—the way computers agree on a single, reliable version of events, even without a central authority.

Why does this matter? You’ll be able to intelligently evaluate and compare blockchain applications—cut through all the marketing BS.

We might be watching new computer science emerge in real time. Cryptography, distributed systems, game theory, and finance are coming together. Chris Dixon’s Read Write Own paints a compelling picture of the impact this technology could have. Messari’s yearly reports also break down blockchain applications, including their 2024 theses.

Blockchain isn’t just about cryptocurrencies. It's a programmable computer no one owns, with no gatekeepers. You don’t need permission to use it. Cryptocurrency is just a tool to reward those who help maintain the protocol—it’s not the end goal.

Blockchain Stack

One representation of blockchain is that it's a stack of four layers:

Note that this is just one taxonomy that's constantly in flux.

Digital Signature Schemes

Blockchains need security without a central authority. Digital signatures provide this by enabling verifiable ownership and preventing tampering.

Digital signatures work because they're asymmetric. If you have the private key, you can sign. If you have the public key, you can verify. The math ensures no shortcuts exist - the possible keys grow exponentially with length, making guessing futile even with all our computers. Even seeing thousands of signed messages doesn't help forge new ones.

This asymmetry is exactly what blockchains need. When I get a signed message from you, I know it came from you. Not because I trust you, but because it's (almost) mathematically impossible for anyone else to create that signature.

Here's the underlying code and math powering Bitcoin's digital signatures, if you're curious to peek under the hood. 3blue1brown also explains it.

// 1. Key Generation
def generate_keypair():
   // Using y^2 = x^3 + 7 (Bitcoin's curve)
   // Points on curve have nice mathematical properties
   // Private key: random k 
   // Public key: k*G (G is special point everyone knows)
   // Like k=2, public=(2,3) means everyone knows 2G=(2,3)
   // But finding k from k*G is hard - this is our security
   private = secrets.randbelow(CURVE_ORDER) 
   public = multiply_point(G, private)
   return private, public

// 2. Signing 
def sign(message, private_key):
    // Need: random number nobody can guess
    // Also need: way to combine message + private key that's:
    // - Unique for each message
    // - Can only be made with private key
    // - Can be verified with public key
    // Solution: r = random*G (like a temporary public key)
    //          s = (hash + r*private) / random
    random = secrets.randbelow(CURVE_ORDER)
    r = multiply_point(G, random).x
    s = (hash(message) + r * private_key) * pow(random, -1, CURVE_ORDER)
    return (r, s)

// 3. Verification
def verify(message, signature, public_key):
    // Need to check s was made with private key
    // Rearrange signing equation:
    // random*G = (hash/s)*G + (r/s)*public
    // If true, signer must know private key
    r, s = signature
    w = pow(s, -1, CURVE_ORDER)  // 1/s
    u1 = hash(message) * w       // hash/s
    u2 = r * w                   // r/s
    point = add_points(multiply_point(G, u1), multiply_point(public_key, u2))
    return point.x == r

There is a great explanation here.

The SMR Problem

State Machine Replication (SMR) is central to distributed systems like databases and blockchains. Its goal: ensure multiple computers stay in sync by following the same sequence of operations.

A classic example is managing a replicated database. Take IBM, which promises 99.999% uptime. When a customer updates one copy, the others must sync perfectly (same state) to ensure consistent query results, no matter which machine is accessed. “State” refers to the system’s current condition where in databases, its the stored data, and in blockchains, it account balances or smart contract statuses. Each operation: database (update record) or blockchain (transferring funds) transforms this state.

While the underlying mechanism is similar, the motivations differ: Traditional databases like IBM's use replication primarily for reliability and uptime while blockchains replicate data to achieve decentralization, ensuring no single entity controls the system.

Here’s how it works:

1. Node runs consensus protocol and process client transactions.
2. Each node maintains an append-only transaction history.
3. Upon receiving a message, a node 3.1) updates its local state 3.2) performs computations 3.3) sends messages to other nodes.

Transaction order is crucial. For example, blockchains must resolve conflicting transactions to prevent double-spending.

To function, SMR guarantees:

1. Consistency: All nodes must eventually synchronize to the same transaction history.
2. Liveness: All valid transactions will eventually be recorded.

Dolev-Strong Protocol

Node Failures and Fault Tolerance

In distributed systems, keeping nodes in sync isn't just about coordination—it's about handling failures and malicious behavior. An honest node follows the protocol without deviation, but in reality, nodes can fail or misbehave in various ways. The different types of faults, from least to most dangerous are:

1. Crash faults are the simplest: imagine someone pulling the plug on a node. Up until the crash, it follows the protocol perfectly, then simply vanishes from the network.
2. Omission faults are trickier: the node might skip sending certain messages. Whether due to network issues or intentional behavior, it doesn't create fake messages—it just stays silent sometimes.
3. Byzantine faults are the worst offenders. A Byzantine node can do anything—send fake messages, send different messages to different nodes, or behave completely unpredictably.

Challenge of Byzantine Faults

Byzantine faults fundamentally change distributed systems. When nodes can't be trusted, even basic operations become complex. This is especially critical in blockchains, where malicious nodes might try to validate fake transactions worth millions. To handle this, protocols typically allow up to "f" Byzantine nodes while still functioning correctly. Beyond "f" faulty nodes, the system can't guarantee correct operation. In this hostile environment, protocols must ensure:

• Honest nodes make consistent decisions despite conflicting information
• The system progresses despite crashes or message omissions
• Malicious behavior is detected before corrupting system state

This need for Byzantine fault tolerance motivates more sophisticated protocols. But first, let's see why simpler approaches fail...

Lazy SMR Protocol

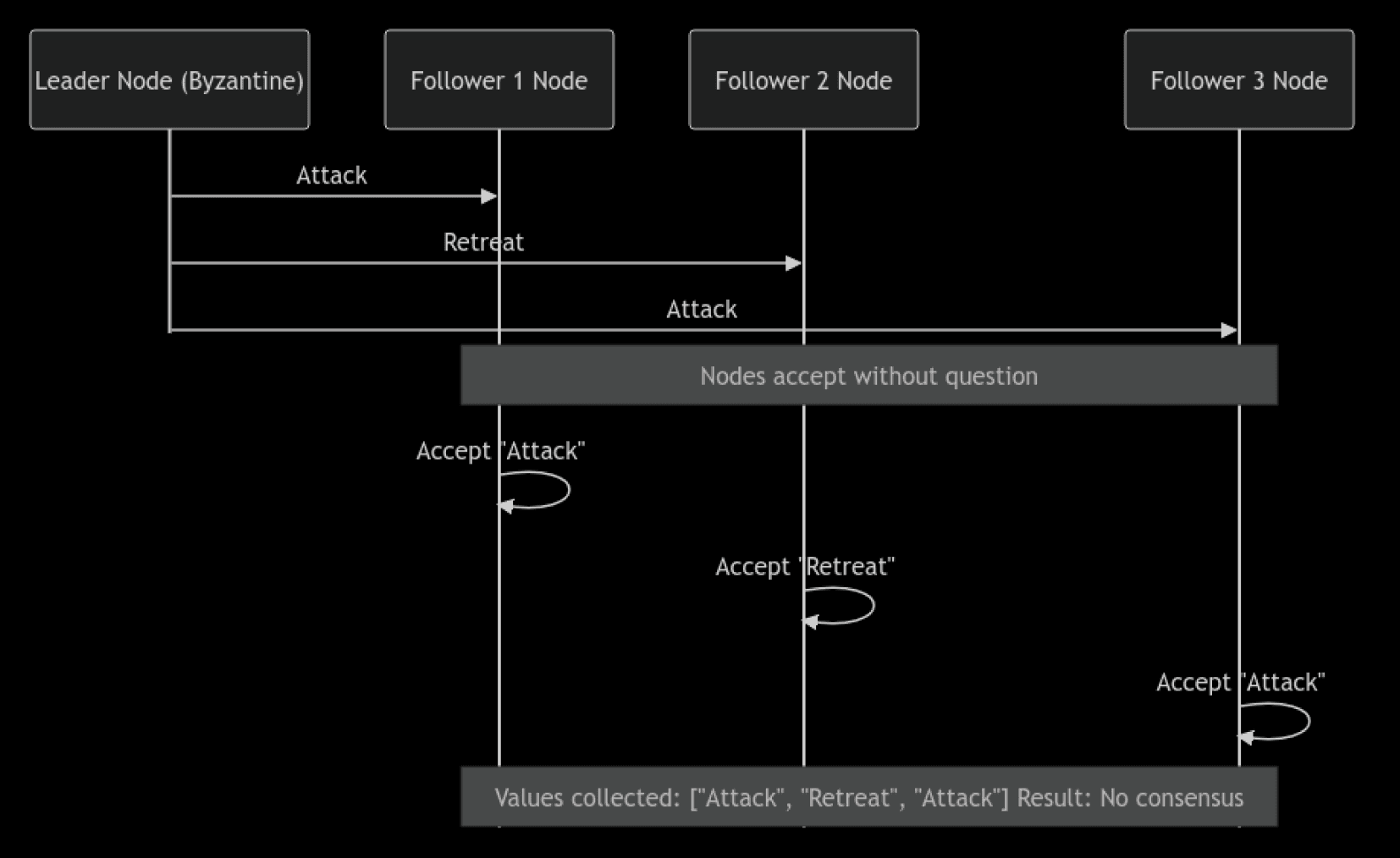
What it is: The lazy SMR protocol assumes that a leader (a node) simply broadcasts its decision, and all other nodes agree without question. It’s like having one person always make the decision for everyone, without cross-checking.

Why it fails: This approach fails because if the leader is faulty or malicious (a Byzantine node), it can send different or false decisions to different nodes. Without a way for nodes to verify what others received, they can’t reach consensus. The system becomes vulnerable to a single bad actor.

Round Robin Protocol

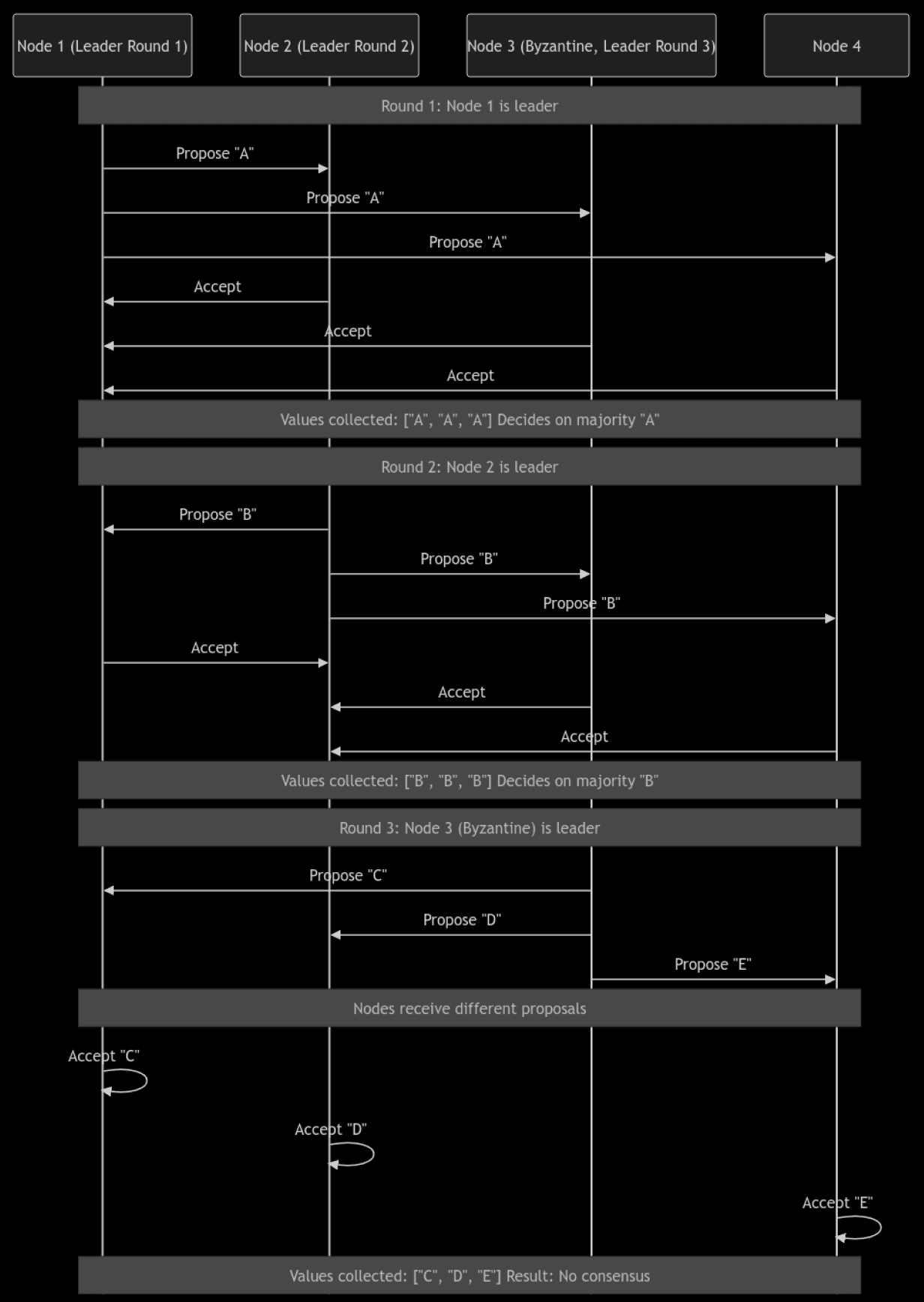
What it is: To avoid relying on a single leader, this method rotates the leader role among nodes. Each node takes turns proposing a decision, and others vote on it. This spreads responsibility and reduces the risk of one faulty leader causing problems over time.

Why it fails: If Byzantine faults are present, a malicious leader in its turn can still disrupt consensus by sending different values to different nodes. Even with leader rotation, the protocol lacks mechanisms to detect or correct this misbehavior.

Byzantine Broadcast Problem

The Byzantine Broadcast Problem deals with how to get all honest nodes in a distributed system to agree on the same message, even when up to f nodes are faulty or malicious. The goal is simple: make sure every honest node receives the same message.

The difficulty comes from the fact that faulty nodes can:

• Send different messages to different nodes.
• Pretend to be other nodes, unless messages are authenticated.
• Collaborate with other faulty nodes to mislead the honest ones. Despite these challenges, the protocol has to ensure that all non-faulty nodes end up with the same, correct message, regardless of what the faulty nodes do.

The more formal way to define it is:

System Model:

• A network of $n$ nodes, where up to $f$ nodes may be Byzantine faulty ($0 \leq f < n$).
• Communication is synchronous; messages sent at time $t$ are received by time $t + 1$.
• Nodes have unique identifiers and can communicate directly with each other.

Roles:

• Sender: A designated node with a private input value $v^*$ from a set $V$.
• Non-senders: The remaining $n - 1$ nodes.

Objective:

Design a protocol satisfying the following properties:

1. Termination: Every honest node $i$ eventually decides on an output value $v_i \in V$.
2. Agreement: For all honest nodes $i$ and $j$, $v_i = v_j$.
3. Validity: If the sender is honest, then for all honest nodes $i$, $v_i = v^*$.

Dolev-Strong

The insight of the Dolev-Strong protocol is using signature chains to catch Byzantine nodes trying to cheat. When a node receives a value, it needs more than just the sender's signature to believe it. The protocol builds up trust gradually over time.

Why this works: When a node sees a legitimate value, it adds its own signature and shares it around. As time passes, nodes expect to see more signatures on legitimate messages. By the end, a message must collect signatures from enough different nodes to prove it's real.

Similar to gathering witnesses, the more people independently confirming that they saw the same thing, the more believable it is. Signature chains are just independent confirmations. This makes it impossible for the Byzantine sender to trick the nodes. And because the protocol runs in the synchronous model where messages arrive on time, honest nodes always have enough time to share what they've learned with each other.

There is a more technical writeup here.

On Impossibility Results

The FLM impossibility result shows that under certain assumptions, no Byzantine broadcast protocol can guarantee all three properties: termination (every node eventually makes a decision), agreement (all nodes arrive at same decision), validity (decision reflects honest nodes' inputs).

There are two core elements to the proof:

1. Simulation: Adversaries can mimic honest nodes.
2. Indistinguishability: Honest nodes cannot differentiate between scenarios.

Just like Turing's halting problem proof, impossibility results: define what’s achievable (which compromises are unavoidable) and guide protocol design trade-off.

Simulation

Indistinguishability

PKI

Asynchronous Model

FLP Impossibility Theorem

Partially Synchronous Model

33%

CAP Principle

Tendermint Protocol

Longest-Chain Consensus

Permissionless Consensus

Proof-of-Work

Selfish Mining